Advent of Code Tricks
Update
I shared this post on Reddit and there’s some nice discussions in the comments section for more tips!
Advent of Code
Last year I discovered and participated in Advent of Code (AoC from here on) for the first time. I had already the same year solved some 500+ HackerRank puzzles and was already in the game of this kind of programming. What’s extra fun with AoC is the surrounding story, the mission to save Christmas in some way, and the community at Reddit with memes and possibility to learn from how other participants solved the problem.
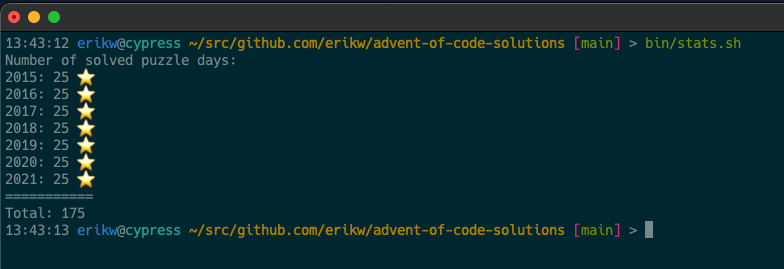
Since solving the AoC 2021 challenge, I’ve had a lot of fun catching up on the previous year’s (first one was in 2015). In less than 11 months I did 7 years of AOC each 25 puzzle-days meaning 175 puzzles in total. According to cloc(1) this was 12.947 Ruby SLOC. It was a lot of fun! Many thanks @topaz :-)
My solutions can all be found at my GitHub repo erikw/advent-of-code-solutions.
After doing the AoC challenges, I’ve picked up some coding tricks that makes solving these challenges easier when they apply. I don’t claim to have come up with any of them, I’ve learned a lot (!) from studying other participants posted solutions. I’ve started to collect these in a document to 1) remember them 2) share with other advent coders. The second point is the purpose of these blog post.
Tricks
Input Parsing
- Integer scanning
- If the input are just integers, instead of parsing or using a complex regex, just scan each integer.
- Example of input: a list of coordinates
<x=-1, y=0, z=2> <x=2, y=-10, z=-7> <x=4, y=-8, z=8> <x=3, y=5, z=-1> - Then just:
input = ARGF.each_line.map do |line| line.scan(/-?\d+/).map(&:to_i) end - Examples: 2018/10
- Load as YAML
- Does the input look like a known format we have parse libraries for? Massage it an load it!
- Examples 2017/25
Testing
Performance testing
Typically you will have several competing ideas, implementation and data structures for your solution. Big-o-theory is one thing, reality might be another. It’s easy to get some runtime stats with time(1). However just a single run is not reliable to make a call about the performance. You need to run it multiple times and take an average. This is where the excellent program multitime(1) comes in! Just give it the number of times it should execute your program and it will give you the time stats:
$ multitime -n 5 ./part2.rb input # Here running solution for 2019/24 for my input.
2031
2031
2031
2031
2031
===> multitime results
1: ./part2.rb input
Mean Std.Dev. Min Median Max
real 12.623 1.343 11.405 12.093 14.958
user 11.808 0.817 11.032 11.640 13.282
sys 0.284 0.051 0.239 0.248 0.369
Now just do the same with your alternative solution and compare!
File naming
The problem instructions often includes several examples with expected results. Sometimes directly and some times after a few hand-calculations. To make the solution development easier to develop and test, save these in some files. The convention that I’ve landed in is
-
input- the raw inputcurl(1)‘d from the website -
input1.X- Input example number X for part 1 -
output1.X- Output expected forinput1.X -
input2.X- Input example number X for part 2 -
output2.X- Output expected forinput2.X
Being precise and following this convention, it’s now super easy to run all tests for one part. Let’s say there were 4 examples for part 1, then we can simply do (an old trick from a University professor in algorithms that I had) in a Bourne-like shell:
$ for i in {0..4}; do ./part1.rb input1.$i | diff -y - output1.$i; done
31 31
165 | 168
13312 | 23312
180697 180697
2210736 2210736
to get side-by-side comparison between expected (column 1) and actual (column 2)! In the above example, two test cases were wrong.
Grids
- Complex Numbers
- For two-dimensional grids, using complex numbers x+yi instead of (x,y) can be beneficial
- Looking at neighbors by applying a delta is easy:
NEIGHBOURS_DELTAS = [-1, 1, -1i, 1i] pos = 1 + 2i NEIGHBOURS_DELTAS.each do |delta| pos_neighbour = pos + delta ... end - Storing a direction is just the numbers
-1, +1i, +1, -1iinstead of up/right/down/left or north/east/south/west. Rotating the direction is just multiplying with-1i(clockwise) or+1i(counter-clockwise). In this examplex == real == rowandy == imag == col. When x and y are swapped, the rotation goes in the other direction.position = 5 + 7j direction = 1i direction *= 1i position += direction - Examples:2020/2, 2018/13, 2018/22, 2019/03, 2019/11
- Cell neighbours (2 dim)
- When needing to check/recurse on all neighbors of a cell (e.g including diagonal neighbors), just loop on the deltas:
deltas = [-1, 0, 1] deltas.each do |dx| deltas.each do |dy| if grid[x + dx][y + dy] == ... end end end - Examples: 2018/18
- When needing to check/recurse on all neighbors of a cell (e.g including diagonal neighbors), just loop on the deltas:
- Cell neighbours (multi dim)
- With more than 2 dimensions the above method becomes clumsy. Say that you’re solving puzzle variant of Convay’s Game of Life or some maze/grid problem with multiple dimensions. Then a method to calculate the direct neighbors in 4 dimensions might look like this using the above method:
DELTAS = [-1, 0, 1] def neighbour_positions(pos) positions = [] DELTAS.each do |dx| DELTAS.each do |dy| DELTAS.each do |dz| DELTAS.each do |dw| delta = [dx, dy, dz, dw] pos_n = pos.zip(delta).map { |a, b| a + b } next if pos_n == pos positions << pos_n end end end end positions end - This is rather clumsy, so let’s make the number of dimensions a parameter to the method instead.
def neighbour_positions(pos, dimensions) deltas = dimensions.times.map { [-1, 0, 1] }.inject(&:product).map(&:flatten).reject { |d| d == [0] * dimensions } deltas.map do |delta| pos.zip(delta).map { |a, b| a + b } end end - Examples: 2020/17 part2 with 2020/17 lib
- With more than 2 dimensions the above method becomes clumsy. Say that you’re solving puzzle variant of Convay’s Game of Life or some maze/grid problem with multiple dimensions. Then a method to calculate the direct neighbors in 4 dimensions might look like this using the above method:
- Easier bounds checking
- In grids/maze algorithm’s you will be at a certain position (x,y) and need to look at all neighbors around you to evaluate the next action. Above shows that it can be made simpler by iterating over products of deltas. However when you have the positions of all the neighbors, you need to check if these are all inside the boundary of the grid. Otherwise your algorithm will take the wrong action or simply go out of bounds of the matrix. Two simple ways to solve this:
- Allocate an outer rim along the matrix that are all walls/empty or whatever NOP-type the puzzle has. That way when you generate neighbor positions they will always be valid but no-action!
- Original maze:
#..##..# .#..#..# #...#..# ###....# ####.### - Wall-enhanced maze:
########## ##..##..## #.#..#..## ##...#..## ####.....# #####.#### ##########
- Original maze:
- Alternatively instead of using an array of array (matrix) as data structure, use a hash map with the default value for keys not in the map being wall/empty. This is what I typically do.
- Sparse grids
- Some problems require grids of possibly large difference in coordinates (these infinite space puzzles) and here an array-based storage won’t cut it. Instead use a hash map with the keys being coordinates and the values the cell value.
- The problem then arises: how do you visually inspect a grid represented as a hash map? If the grid dimensions are reasonable, I usually manage by making a helper method like this:
def print_map(map, pos_cur = nil) xmin, xmax = map.keys.map(&:real).minmax ymin, ymax = map.keys.map(&:imag).minmax (xmin..xmax).each do |x| (ymin..ymax).each do |y| pos = Complex(x, y) print pos_cur == pos ? SYM_POS_CUR : map[pos] end puts end end - Examples: 2019/20
-
Hex grids
- When the problem is about hex grids, using Cube Coordinates can make the problems trivial to solve, as we can use standard vector operations and distance calculations we’re used to in cartesian coordinate systems.
- Examples: 2017/11, 2020/24
Algorithms
- Dijkstra’s Algorithm
- Instead of spending time in a grid to discover all nodes (cells) before Dijkstra as its input, instead add new nodes as they are discovered. If you’re lucky, some time could be saved but not considering all cells.
- Examples: 2018/15
- Recursion
- There’s often opportunity to save alot of resources on caching recursive calls. Make it transparent with a default empty cache as optional argument.
- Examples: 2020/19
Automation
- Scripting problem setup
- You’re going to solve a lot of puzzles and you will save time by scripting as much as you can so that you can spend your energy on the actual problem solving. For me this meant a simple and very specific to me script
solve_day.shthat:- select puzzle to solve: no arguments mean’s today’s puzzle, or argument like
20/7to solve puzzle 2020-07 - create a new directory for the selected puzzle day
- downloads the
inputfor the selected puzzle day - populate empty source files, README.txt etc for the puzzle day
-
$ chmod o+xon the executables - opens up a tmux split pane with my editor + shell to execute and debug in
- open my editor with the right tabs and split windows
- after the editor closes -> assumes the puzzle is solved -> print command ready to copy and paste that git commits with a git message formatted for today’s date.
- prints some simple stats over solved puzzles
stats.sh
- select puzzle to solve: no arguments mean’s today’s puzzle, or argument like
- Python users have a lot of helper libs to automate e.g. input download, parsing and even solution submission.
- You’re going to solve a lot of puzzles and you will save time by scripting as much as you can so that you can spend your energy on the actual problem solving. For me this meant a simple and very specific to me script
Misc
- Constraint solver
- Grammar parsing
- When the task is to parse a grammar. Instead of implementing a parser self, transform the input to the format of a common parser generator and let it generate a parser for it
- Examples: 2020/19
- Eval
- If there’s an expression, maybe arithmetic, that needs to be evaluated. If your language has an
evalmethod to evaluate a string in the same language, transform the input and eval it! - If you’re language allows, you could take some shortcuts and redefine some operators (see 2020/18 below).
- Examples: 2020/18
- If there’s an expression, maybe arithmetic, that needs to be evaluated. If your language has an
Ruby
- throw-catch
- Deep cloning next state version
- In recursions that need a complete copy of a state, or when we iterate on something like a grid that needs to be updated in multiple steps using current values, make a complete copy of the state with deep cloning. *
5.times do map_next = Marshal.load(Marshal.dump(map)) (0...map.length).each do |x| (0...map[0].length).each do |y| map_next[x][y] = something_with(map) end end map = map_next end - Examples: 2018/18, 2015/18
- In recursions that need a complete copy of a state, or when we iterate on something like a grid that needs to be updated in multiple steps using current values, make a complete copy of the state with deep cloning. *
Closing
The latest version of my collected tricks can be found at tricks.md





Leave a comment
Your email address will not be published. Required fields are marked *